Power System Reliability Considerations

Note: Page needs rewriting. Do you want to contribute?

Introduction

The power system is an essential part of every flying device. If the power system fails then our beloved flying platform will fall out of the sky, and sometimes the damages can even include our calibrated air data instrumentation! The solution is a redundant power system. We will discuss here on the reliability of a range of commonly used power system layouts.

RC Big scale flying wing Focke Wulf 3×1000 (31 kg). High reliability is needed here.

Prior to considering the performance of any layout we will first discuss the reliability of a battery pack alone. Battery packs are composed by single cells, connected in series or in parallel.

There are different technologies on batteries cells, for example LiPo, NiCd or NiMh. Our reliability considerations are independent of the battery technology.

As users we’re interested to know when a battery cell will fail. In other words, we want to know whether the battery will be correctly operating during the impending 15-minute-flight. A closed-form solution for such an answer is not in our reach. Even the manufacturers of the cell are not able to provide that form of reliability information to the users.

Figure 1 – Focke Wulf 3×1000. Redundant power system.
The engineer went to great extends to ensure reliability by installing of two independent receivers.

The main reason is that every battery, after leaving the factory, is exposed to different environmental conditions and workload. Such a fact degrades, or even invalidates, any experimental data gathered during the lab tests on sample batteries.

In many appliances such as UPS’s, a mechanism which estimates the health status of the battery based on real time data may be present.

Unfortunately, this kind of estimation systems usually can’t provide accurate short-term predictions. As worrisome as it can be, it is possible to charge a battery, have it perform flawlessly, with a 100% nominal charge, and the very next flight it can fail.

That is because the possible causes of battery failure are a many and different in nature, and of course they are also technology dependent. The most used workaround for lack of reliable information, in mission critical system such as ours, is redundancy.

Figure 3 – Diode based circuit that protects the power system from single cell short circuit

It’s worth our attention to find a relationship between the single cell reliability and the battery pack reliability. To that goal, we will introduce some statistics concepts. Let’s define the reliability of the cell $i$ as $R(\tau)_i$ , $\tau$ represent the length of a time interval. Writing $R(\tau)_i=0.96$ we state that with a probability of 96% the battery will operate properly in the next $\tau$ hours interval of time. From now on we will assume, as a simplification, that $\tau$ has a constant value so we will write $R_i=0,96$ .

Let’s suppose that we have a battery pack $b_1$ composed by $n=2$ identical cells in series, as depicted in figure 2. The overall reliability is $R_{b_1}=(R_1)^n=(R_1)^2$ , if the reliability of the single cell is 0.96 then $R_{b_1}=0.9216$ .

Figure 2 – From top to bottom: Series connection, parallel connection and parallel of series connection

A series component has a combined reliability that is lower than the single cell reliability, look the table 1.

Now we evaluate the reliability of a pack that is composed by two identical cells in parallel connection $R_{b_2}=1-[(1-R_1)\cdot(1-R_2)]=0.9984$ .

Regarding reliability, the more cells in parallel the better.

If we connect two $R_{b_1}$ packs, composed by two cell in series, in parallel the reliability of the assembly is $R_{b_3}=1-[(1-R_{1})^2]=0.9938$ .

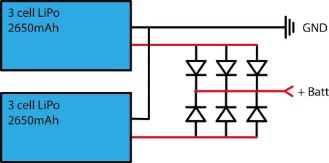
So a parallel configuration can mitigate the reliability loss introduced by a series configuration. Keep in mind that for a full redundancy the two parallel cells/packs should have the same nominal capacity and the circuitry configuration should warrant that failure of one cell/pack does non implicate the failure of any other element (a simple solder joint will fail to do so). Refer to figure 3 for a basic diode based circuit that avoid total failure of parallels batteries packs.

To note in Figure 3 that that circuit cannot protect the battery if there is a load short circuit. For example is you have a shorted servo or servo line short the battery will short.

Besides the exact value of reliability and dedicated circuitry design we’ve demonstrated how we can affect the reliability performance of a battery pack with series and parallel layouts. However, we’d still like to know how will our battery fail The life cycle of a battery is sometimes represented with a bathtub curve diagram (Figure 4).

To note in Figure 3 that that circuit cannot protect the battery if there is a load short circuit. For example is you have a shorted servo or servo line short the battery will short.

Table 1

CELLS	RELIABILITY
1	96.0 %
2	92.2 %
3	88.5 %
4	84.9 %
5	81.5 %
6	78.3 %
7	75.1 %

When the cell is new it is possible that it has some fabrication-related defects, that will be observed in the first charge-discharge cycles. If the cell passes the early failure phase, it then enters a long operational life phase, characterized by low failure rates. At the end of the operational life phase, the wear out phase ensues, which is ended by the cell failure.

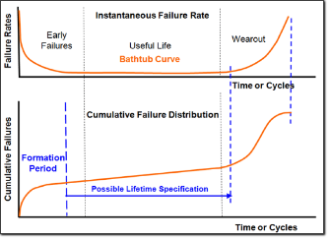
Without going into details and using a common approach, the failures types can be categorized in three different sets. Infant mortality is any fail in the early stage of battery life, wear-out is any fail caused by the aging and use of the battery and the random faults are the faults that can be present at any point of the life cycle.

The most dangerous failure constitutes in an internal short: The cell temperature can increase up to ignition temperature. That will lead to fire into the airframe, see Video 1. From an electrical point of view, a short always results in a total failure of the battery pack. On a single battery pack powered aircraft, this is equivalent to the total loss of thrust and control, usually resulting to a catastrophic crash. If redundant systems are present, usually the power to control surfaces and electronics is guaranteed but the main electrical engine may be not powered.

The minimum requirement for a redundant system should be that the vehicle has the ability to be comfortably commanded to a crash land.

Single BEC vs redundant configurations

Video 1 – RC plane landing on flames, of course a dreadful spectacle

We will examine the power system of a model airplane from the aspect of reliability. Now we examine a single BEC configuration against to a couple of typical redundant configurations. Common equipment configurations will be used as examples.

In a vehicle where the primary power source are electric batteries, the most crucial power consumers are the motor, the avionics and the servos. From now on, for the sake of simplicity, we will refer to the powerplant of the aircraft (which is tasked with producing thrust) as the “thrust” system, whereas the rest of the electric power consumers on the aircraft will be called the “control” system.

Table 2

CASE	Batt.P	Batt.C	ESC	BEC
1	Fail	Fail	Fail	Fail
2	Fail	Fail	Ok	Fail
3	Fail	Fail	Fail	Ok
4	Fail	Fail	Ok	Ok
5	Ok	Fail	Fail	Fail
6	Fail	Ok	Fail	Fail
7	Ok	Ok	Fail	Fail

We will carry out a high level analysis, since too much detail would eventually distract the reader from the most relevant factors.

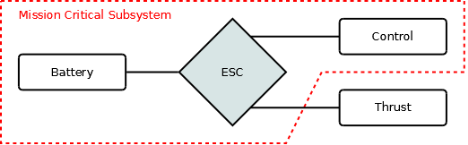
Refer to Figure 6: our first layout consists of a single battery pack connected to the ESC. Control and thrust are powered by the ESC. Our working hypothesis is that the different failures modes can be considered independent.

Let’s select the battery pack reliability value at $R_p=0.96$ and the reliability value of the ESC at $R_{ESC}=0.98$ . The battery and the ESC should be working at the same time, so for the first layout, the reliability is $R_{l1}=R_p \cdot R_{ESC}=0.940$ .

We notice that the overall reliability is lower than the reliability values of each single component. Moreover, our system is not redundant, since the failure of each component causes the failure of the overall system. Our second layout consists of two independent batteries, one for thrust and one for control. One battery is physically connected to the motor’s ESC and the other is connected to a BEC circuit that supplies the control module.

Usually, the power related to the thrust system has more capacity and nominal voltage than the control battery.

Let’s set the reliability value of the battery packs to $R_p=R_c=0.96$ , the reliability value of the ESC to $R_{ESC}=0.98$ and the reliability of the BEC to $R_{BEC}=0.98$ . Under nominal system operation, the two batteries, the ESC and the BEC should be operational at the same time. From this aspect, the reliability of the second layout is $R_{l2}=R_p\cdot R_{ESC}\cdot R_c\cdot R_{BEC}=0.885$ . At first, this result seems wrong: Despite having used more equipment, the overall reliability is now lower than the initial 0.940 value from Layout 1. Until now we haven’t considered in detail what happens when a part of our system fails and that led us to non-comparable results. In fact, under careful examination, the second layout has extended capabilities. In layout 1 we have a probability $1-R_{l1}=0.06=6\%$ of a total power loss, and if this unfortunate event happens then we will lose control of the vehicle as well as any ability to safely (crash) land the unit. Revisiting Layout 2, we calculate the probability to lose completely the vehicle control.

The cases that lead to a catastrophic failure are those that include a simultaneous failure of both the batteries or both the ESC and BEC. The Table 2 presents all such failure cases.

Combining the probabilities of the cases indicated in the table, we get the following expression for reliability:

$R_{l2flat} &= 1-((1-R_p)\cdot(1-R_c)+(1-R_{ESC})\cdot(1-R_{BEC})) \\ &= 1-(0.0016+0.0004)=0.998=99.8\%$

Figure 6 – Layout 1: Single battery system

Now the odds changed to being favorable to Layout 2. However from a user’s point of view, it is more interesting to know the value of the probability that the vehicle is still controllable (at least to some degree) after a failure. The necessary condition for controllability is that the BEC and its battery are still working properly.

Refer to the next Table 3. In cases 8 to 11 the pilot will have a chance to land the aircraft safely.

The reliability related to this minimum guaranteed performance is $R_{l2user}=R_c\cdot R_{BEC}=0.940$ .

This value is the same as the value of the first layout. With this method of analysis, the advantage of Layout 2 over Layout 1 not so clear anymore. However, the situation can be radically different if there is a relationship between the reliability of batteries/ESC/BEC and the corresponding capacity/max-current/etc or there is a dependency among the reliabilities of single items.

Figure 7 – Layout 2: One battery for thrust, one battery for control

All things said, however, by inspection of Layout 2, it is evident that it does not offer any physical redundancy, so statistics apart, it’s wise to not expect any sudden reliability increase.

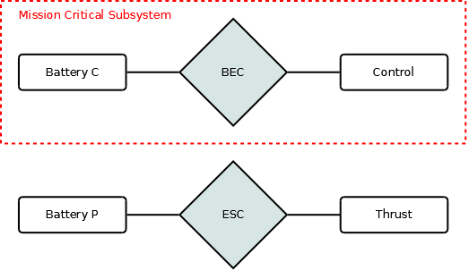
In the layout number 3, we have a battery that goes straight to the ESC and a redundant voltage regulator, powered by two separated batteries, which feed the control system. The working hypothesis is that the redundant voltage regulator will continue to work even if one battery fails. The most tricky failure to handle for the voltage regulator is a battery cell short. Fortunately even regulators at RC grade can handle this condition[1].

Back to the math, this layout is more reliable as the system composed by voltage regulator with $R_v=0.98$ and two batteries with $R_c=0.96$ .

$R_{l3} = 1-((1-R_c\cdot R_v)(1-R_c\cdot R_v)) =1-0.0035=0.996=99,6\%$ [2]

Using the same battery pack type, layout 3 offers augmented reliability, and that result was reached by means of physical components redundancy.

Typically, the weakest link in the chain affects the system reliability the most, so prior to purchasing or building an expensive or complex reliable thrust system, an analysis of the reliability of the whole aircraft system should be performed. It will be useless to have an amazing thrust system with undersized servos.

Table 3 – Failure modes that lead to a controllable (crash) land

CASE	Batt.P	Batt.C	ESC	BEC
8	Fail	Ok	Fail	Ok
9	Ok	Ok	Fail	Ok
10	Fail	Ok	Ok	Ok
11	Ok	Ok	Ok	Ok

References

[1]
Smart-Fly, “Smart-Fly – PowerSystem Eq6 Turbo Plus – Battery input protected.” Smart-Fly [Online]. Available: https://smart-fly.com/index.php?route=product/product&path=59&product_id=52

[2]
Mc Dowall, “Lies Damned Lies and Statistics: The Statistical treatment of Battery Failures.” www.battcon.com [Online]. Available: https://www.battcon.com/papersfinal2005/mcdowallpaper2005.pdf

Power System Reliability Considerations

Introduction

Single BEC vs redundant configurations

Further Readings

References

0 Comments

Leave a Reply Cancel reply